TP 7 : Classification supervisée : les hyper-paramètres

Dans ce nouveau TP sur les arbres de décision qui fait suite aux précédents, nous étudions comment améliorer la performance des arbres de décision induits sur un jeu de données.

À l'issue de ce TP, vous m'envoyez par email un compte-rendu (format odt ou pdf) indiquant la réponse aux questions qui sont posées. Vous m'envoyez également un fichier python réalisant toutes les manipulations de ce TP. Appelez-le tp7.votre-nom.py. Je dois pouvoir exécuter ce fichier en tapant python3 tp7.votre-nom.py et reproduire vos résultats. Cette exécution ne doit pas provoquer d'erreur de python. Remarque : un notebook ne convient pas.

Introduction

On s'intéresse à un jeu de données concernant le diabète. Au début du TP, nous allons utiliser le jeu de données disponible à cet url https://philippe-preux.codeberg.page/ensg/miashs/datasets/pima-made-easy.csv. Comme son nom l'indique, c'est un jeu de données classiques (pima) que j'ai simplifié.

Il y a 9 attributs : 8 sont quantitatifs et le dernier est la classe : patient diabétique (pos) ou pas (neg). Les 8 autres attributs contiennent l'information suivante :

À faire : vous chargez ce jeu de données et vous commencez par explorer visuellement ses attributs comme on l'a fait avec les olives. (Visualiser la répartition des valeurs de chaque attribut séparément et visualiser ensuite les données en fonction de chaque paire d'attributs en colorant chaque point en fonction de sa classe.) Voyez-vous quelque chose ? Arrivez-vous à trouver quel attribut pourrait être placé à la racine d'un arbre de décision ?

À faire : induire un arbre de décision comme on l'a fait lors du TP précédent. Comme on l'a vu dans le TP 5, estimer son taux de succès sur le jeu de test et son taux de succès moyen et son écart-type avec une validation croisée à 10 plis.

Influence des hyper-paramètres de l'arbre induit

Lors de la création d'un arbre de décision, on peut spécifier la valeur de certains hyper-paramètres qui influencent la manière suivant laquelle l'arbre est construit. Ils peuvent avoir un impact important sur le taux de succès de l'arbre.

En apprentissage supervisé, il faut toujours garder à l'esprit que le plus gros modèle n'est pas toujours le meilleur. Bien au contraire, très souvent, un modèle moins gros possède un taux d'erreur plus faible. C'est le cas avec les arbres de décision : ce n'est pas le plus grand arbre qui prédit le mieux.

On va étudier quatre hyper-paramètres :

Nombre d'exemples minimum associés à une feuille

Le paramètre min_samples_leaf de la méthode tree.DecisionTreeClassifier() indique le nombre minimum d'exemples qui sont associés à une feuille lors de l'induction de l'arbre. Par défaut, cette valeur est 1, ce qui est évidemment bien trop petit : avec un seul exemple d'entraînement par feuille, la feuille prédit la classe de cet exemple et cette feuille risque fort de provoquer du sur-apprentissage.

À faire : on suit la méthodologie vue lors du TP 5. Estimer le taux de succès d'arbres de décision en fixant la valeur de l'hyper-paramètre min_samples_leaf à 5, 10, 15, 20. Quelle valeur donne la plus petite erreur ? Pratiquer de même par rvalidation croisée. Obtenez-vous la même conclusion ?

Mesure d'impureté

Comme on l'a vu en cours, on peut mesurer l'impureté (comment les classes sont mélangées dans un jeu d'exemples) de différentes manières, en particulier avec l'impureté de Gini et avec l'entropie. Le paramètre criterion de la méthode tree.DecisionTreeClassifier() indique la mesure d'impureté à utiliser lors de l'induction. Par défaut, c'est l'impureté de Gini. Pour utiliser l'entropie, on indique criterion="entropy".

À faire : refaites les mêmes estimations pour les 5 valeurs de min_samples_leaf en utilisant l'entropie. Quelle est la meilleure combinaison ?

Profondeur de l'arbre

Le paramètre depth de la méthode tree.DecisionTreeClassifier() indique la profondeur maximale de l'arbre. Ce paramètre permet de limiter la taille de l'arbre.

À faire : en utilisant la paire des meilleurs hyper-paramètres trouvés précédemment, vous induisez des arbres dont la profondeur varie de 1 à 20. Vous estimez leur taux d'erreur/taux de succès. Vous faites un graphique représentant ces taux en fonction de la profondeur. Qu'observez-vous ?

Ci-dessous, un graphique montrant le taux d'ereur mesuré sur un jeu de test en fonction de la profondeur de l'arbre induit :

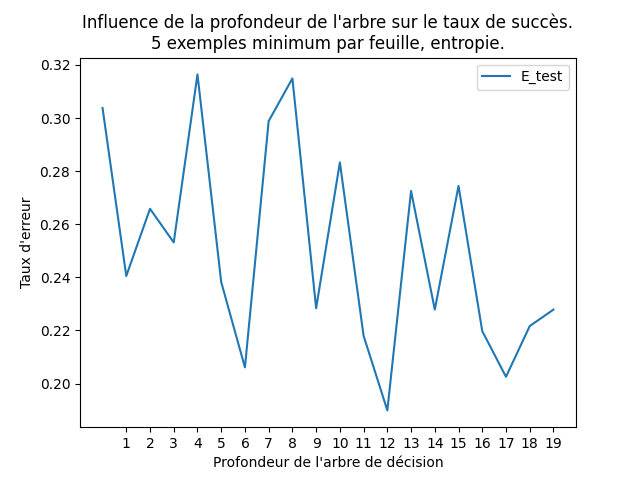
Dans cette figure, outre le paramètre depth que l'on a fait varier, l'arbre est induit avec les paramètres min_samples_leaf = 5, criterion = "entropy". Réalisez ce type de représentation graphique. Ajoutez-y des barres d'erreur correspondant à plus ou moins 1 écart-type.
Le taux d'erreur sur le jeu de test est minimal pour les profondeurs 6 et 12. De manière générale, on a préfère un arbre le plus petit possible ayant un taux d'erreur le plus petit possible. Donc celui de profondeur 6 est un bon compromis.

Sur-apprentissage

On peut voir le sur-apprentissage en pratiquant comme suit : en reprenant ce que vous avez fait ci-dessus, pour chaque profondeur, vous estimez aussi le taux d'erreur sur le jeu d'entraînement. Et vous faites le graphique du taux d'erreur sur le jeu d'entraînement et sur le jeu de test en fonction de la profondeur. J'obtiens ce graphique :

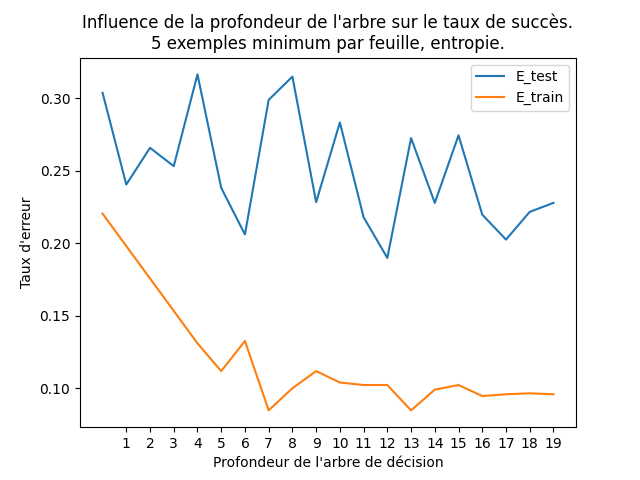
On voit que le taux d'erreur sur le jeu de test a tendance à diminuer jusque la profondeur 6 puis fluctue. Au-delà de la profondeur 7, il y a sur-apprentissage : l'arbre est trop complexe, trop grand, pour ce jeu d'entraînement.
Pour sa part, le taux d'erreur sur le jeu d'entraînement diminue jusque la profondeur 7 et qu'ensuite il remonte et fluctue.
Ce graphique nous pousse également à sélectionner l'arbre de profondeur 6 comme étant le meilleur des arbres qui ont été construits.

La complexité de l'arbre α

Comme on l'a vu en cours, l'hyper-paramètre α permet d'optimiser le compromis entre la taille de l'arbre et son taux de succès. Il vient se combiner avec les hyper-paramètres vus ci-dessus, et d'autres encore dont nous ne parlons pas.

Ayant créé un arbre comme plus haut : 

arbre = tree.DecisionTreeClassifier (les hyper-paramètres que vous voulez, random_state = rs)

on calcule un « chemin d'élagage » à l'aide la fonction suivante : 

chemin = arbre.cost_complexity_pruning_path (Xtrain, Ytrain)

où Xtrain et Ytrain sont un jeu d'entraînement (données et étiquettes, notations habituelles).
L'objet chemin contient deux composantes :

Le premier est une table de valeurs de α qui correspondent à des élagages successifs. La première valeur est 0, ce qui correspond à l'arbre au complet. Plus la valeur d'α augmente, plus l'arbre est élagué et rapetisse donc.
Le principe est de construire un arbre pour chacune des valeurs de α, de mesurer le taux de succès de chacun sur un jeu de test et finalement, de sélectionner l'arbre qui minimise cette erreur.
On spécifie la valeur de α pour construire un arbre de décision en ajoutant l'hyper-paramètre ccp_alpha = α lors de l'appel de la méthode tree.DecisionTreeClassifier().

Donc, en résumé, pour chacune des valeurs de la table ccp_alphas, on construit un arbre de décision en spécifiant cette valeur de α et on estime son taux de succès. Ensuite, on cherche l'arbre qui maximsie ce taux de succès : c'est l'arbre que l'on cherche. Dans cette procédure, il est bon de partir d'un grand arbre, donc de laisser la valeur de min_samples_leaf à sa valeur par défaut (1).

À faire : faites tout cela. Quel est le taux de succès de l'abre obtenu ? Est-il meilleur que celui des arbres construits précédemment ? Quelle est sa taille ? Faites en une représentation graphique.
Là encore, on peut estimer le taux de succès sur le jeu d'entraînement et représenter graphiquement les taux de succès d'entraînement et de test. Voyez-vous apparaître le sur-apprentissage ?

En conclusion

En conclusion de ce TP, on constate que trouver le « meilleur » arbre de décision est une tâche ardue. La notion même de « meilleur » n'est d'ailleurs pas bien claire. Il faut essayer beaucoup de combinaisons, explorer visuellement les données et prendre garde à l'estimation des taux de succès. Et il y a encore bien d'autres points que l'on pourrait étudier pour essayer d'obtenir de meilleurs modèles prédicitfs.

La démarche que nous avons adoptée avec des arbres de décision est la même quel que soit le modèle prédictif en apprentissage supervisée.