TP 6 : Classification supervisée en ouvrant l'œil

Jusqu'à maintenant, on a utilisé des fonctions qui induisent des arbres de décision sans se pré-occuper d'explorer visuellement le jeu de données.
Or, cette exploration que seule un être humain peut réaliser efficacement parce qu'un être humain voit, certaines propriétés lui sautent aux yeux.
Dans cette suite du TP sur la classification supervisée avec des arbres de décision, nous abordons cette exploration visuelle et voyons comment elle permet d'améliorer le modèle de prédiction de classe, ou plus simplement, de diagnostiquer visuellement le modèle que l'algorithme a construit automatiquement.

Cette exploration visuelle est capitale lors de l'étude d'un jeu de données. Son impact sur la démarche et les résultats peut être très important.

À l'issue de ce TP, vous m'envoyez par email un compte-rendu (format odt ou pdf) indiquant la réponse aux questions qui sont posées. Vous m'envoyez également un fichier python réalisant toutes les manipulations de ce TP. Appelez-le tp6.votre-nom.py. Je dois pouvoir exécuter ce fichier en tapant python3 tp6.votre-nom.py et reproduire vos résultats. Cette exécution ne doit pas provoquer d'erreur de python. Remarque : un notebook ne convient pas.

Retour sur la prédiction de l'attribut region

L'arbre de décision construit plus haut commet parfois des erreurs. Nous allons voir une manière de réduire le risque d'erreur.
C'est une méthode très générale qu'il faut absolument connaître et utiliser lorsqu'on utilise des arbres de décision.
Nous allons procéder visuellement car cette manière de faire ne s'automatise pas facilement. Alors que parfois, comme on l'a déjà dit, il y a des choses qui sautent aux yeux.

L'arbre obtenu prédit parfaitement les olives du Sud de l'Italie ; on l'avait déjà vu. Par contre, il ne sépare pas parfaitement les deux autres régions, Nord et Sardaigne. On va donc se concentrer sur les olives de ces deux régions.
Pour cela et pour se simplifier la vie, on peut créer un objet olivesPasDuSud à l'aide d'un filtre logique : lesOlivesPasDuSud = olives.loc [:,"region"] != 1.
Ensuite, on fait des scatter plots de ces olives pour chaque paire d'attributs et en utilisant une couleur indiquant la région. On regarde ces graphiques et on essaie d'en identifier où les olives des deux régions sont séparées. Rappelons-nous qu'un arbre de décision (comme ceux construits par l'algorithme disponible dans scikit-learn que nous utilisons) découpe l'espace de données avec des droites parallèles aux axes, ce qui correspond à des tests du type attribut ≤ valeur. Essayons de trouver une paire d'attributs permettant de séparer les deux classes par une droite.
Avec 8 attributs, nous obtenons 8x7/2 graphiques :
fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig fig

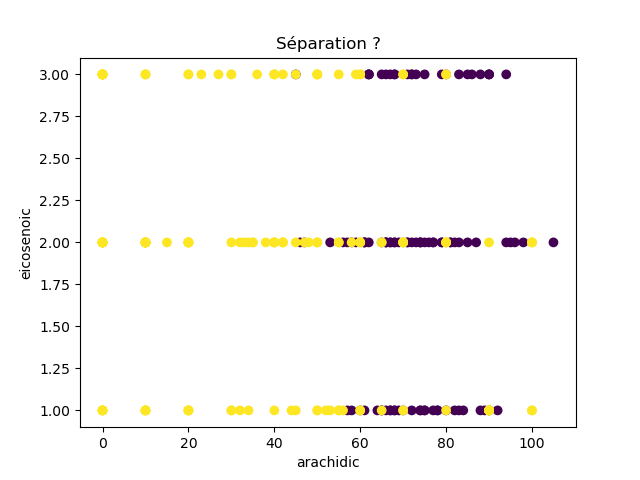
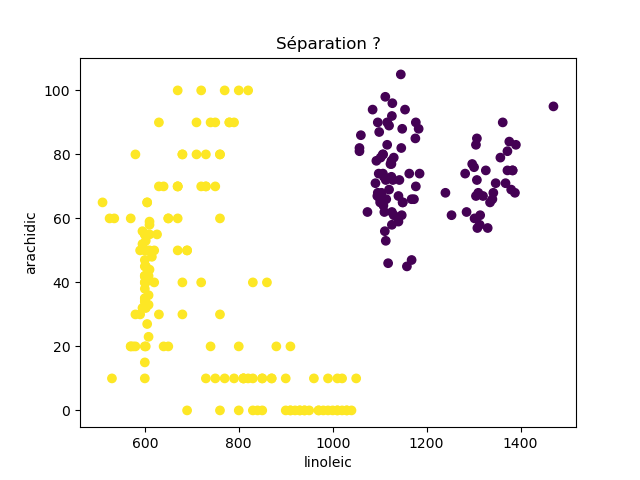
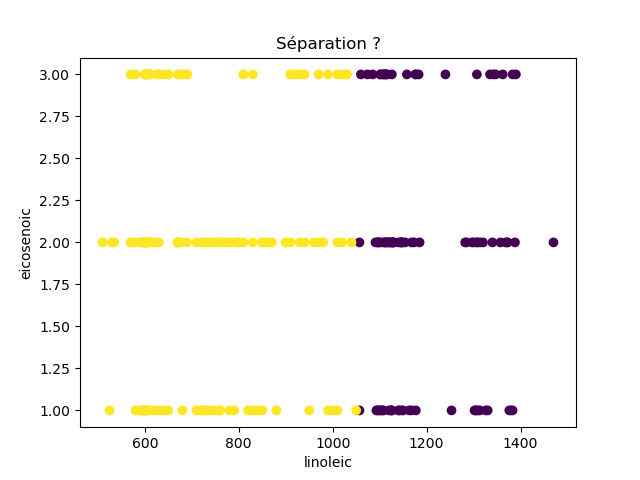
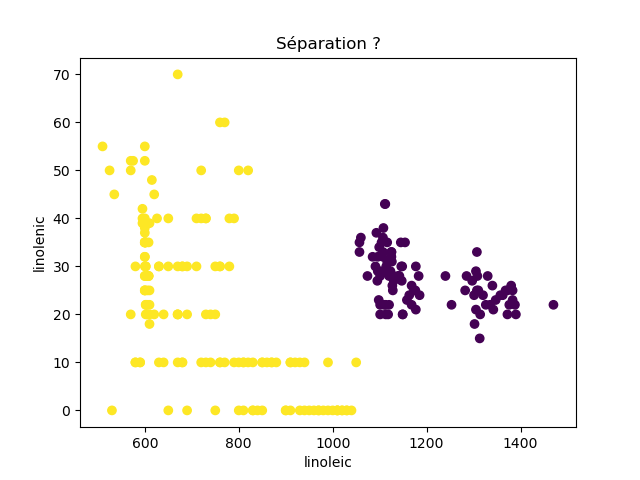
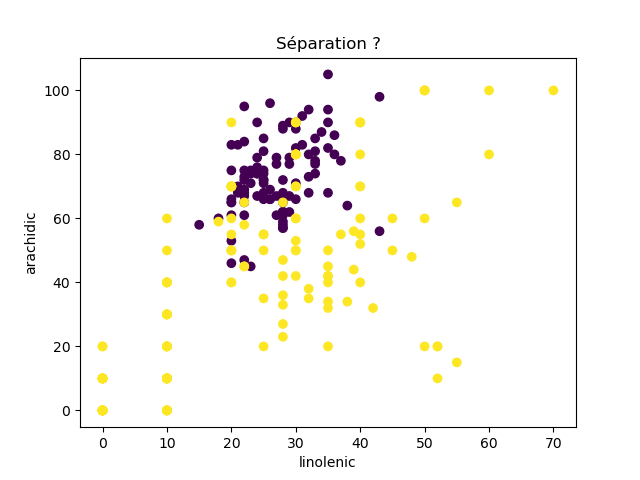
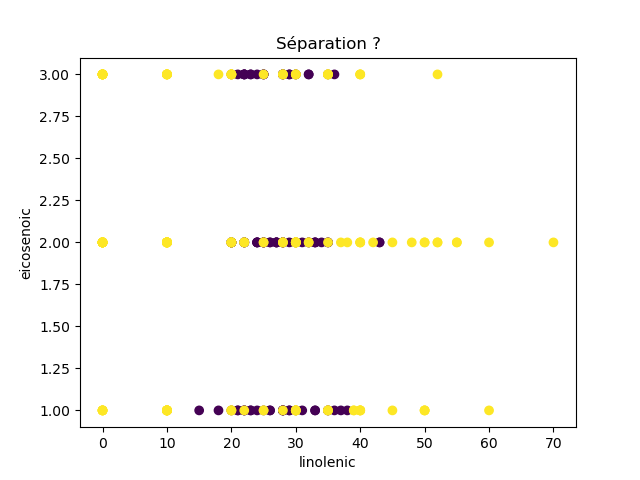
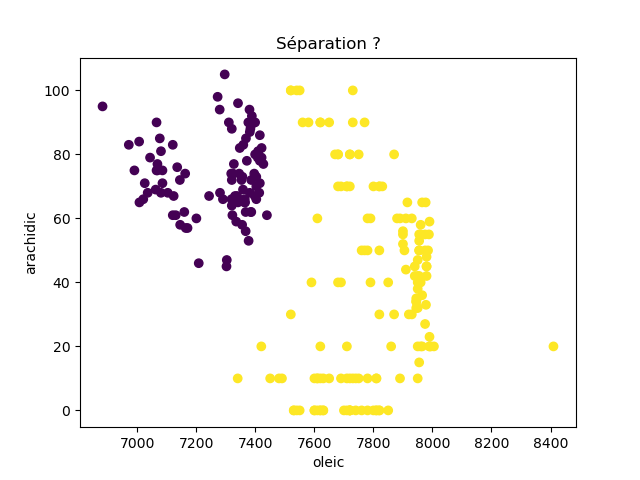
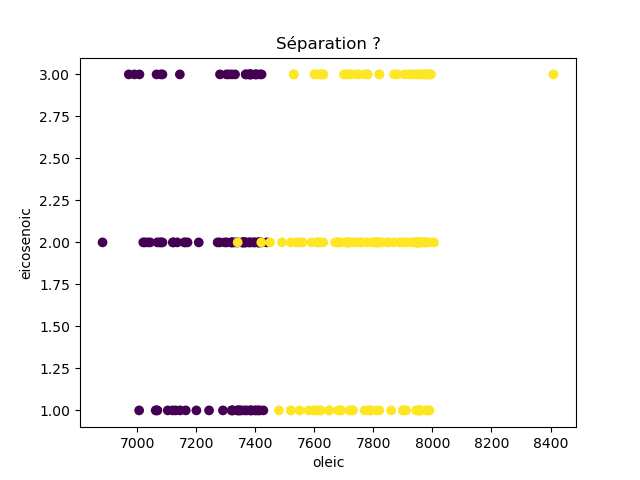
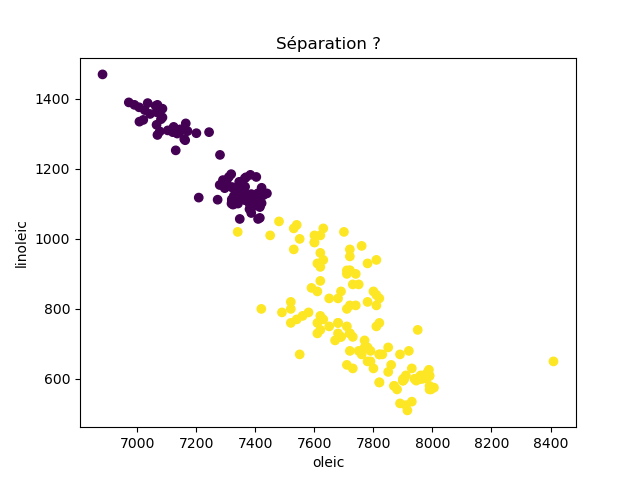
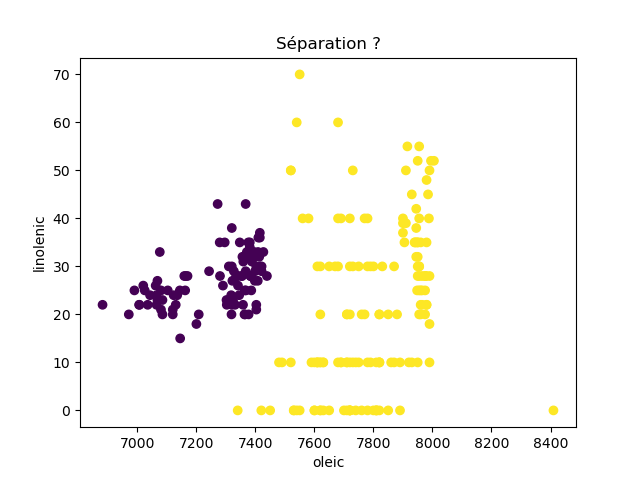
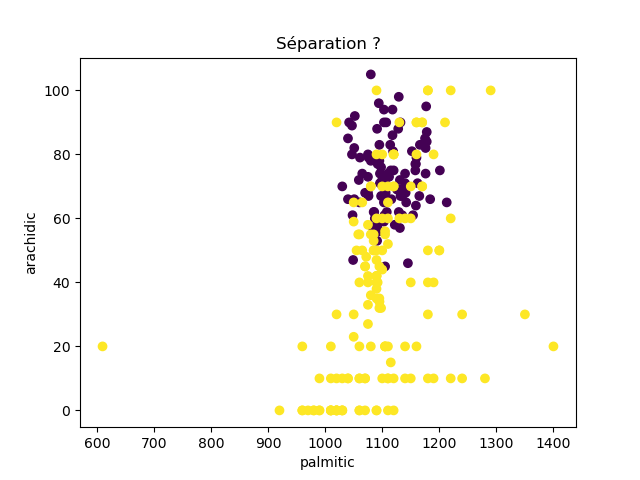
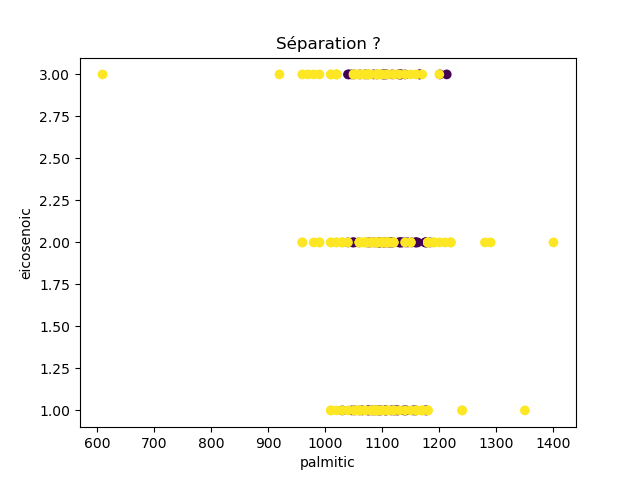
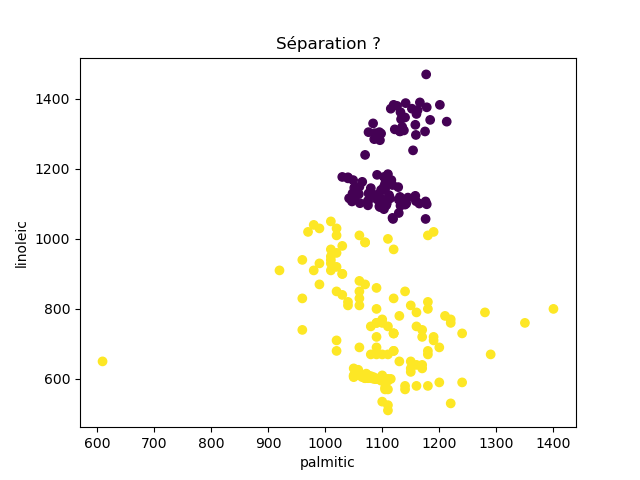
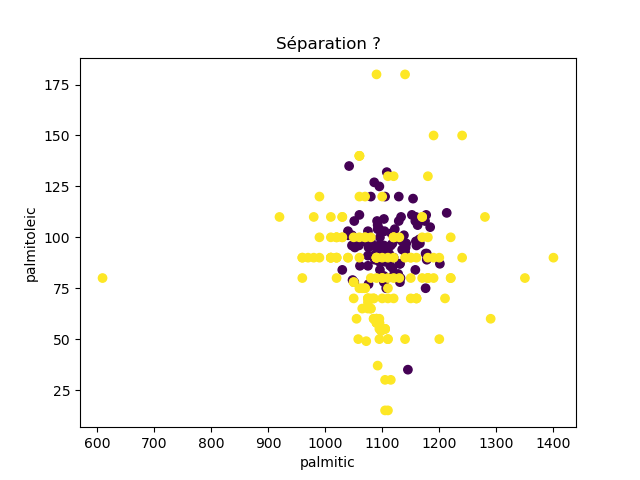
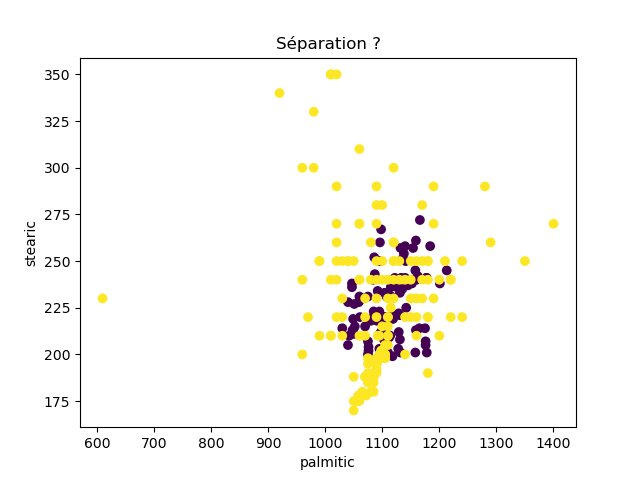
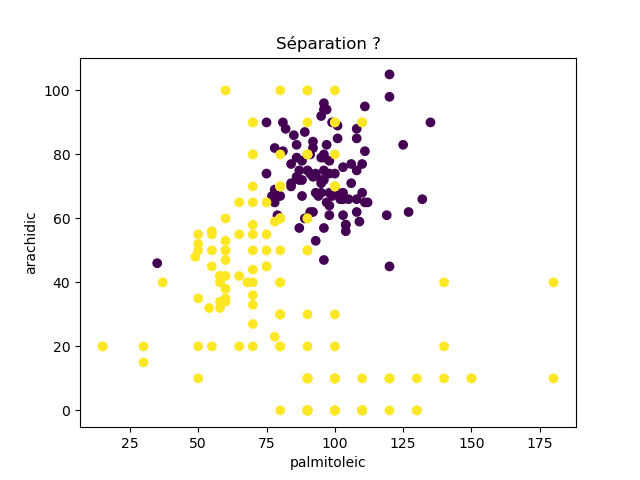
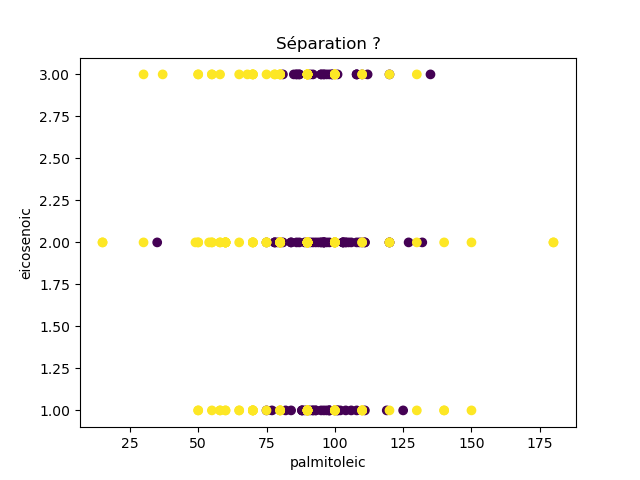
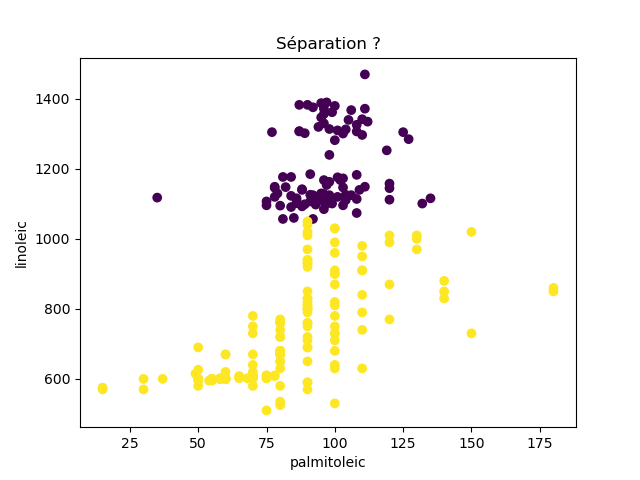
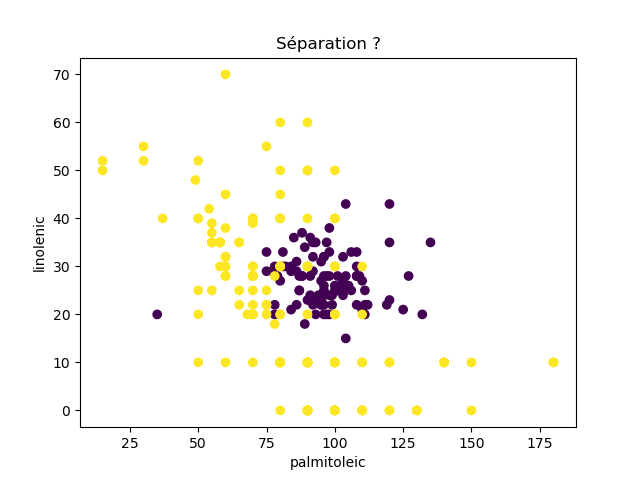
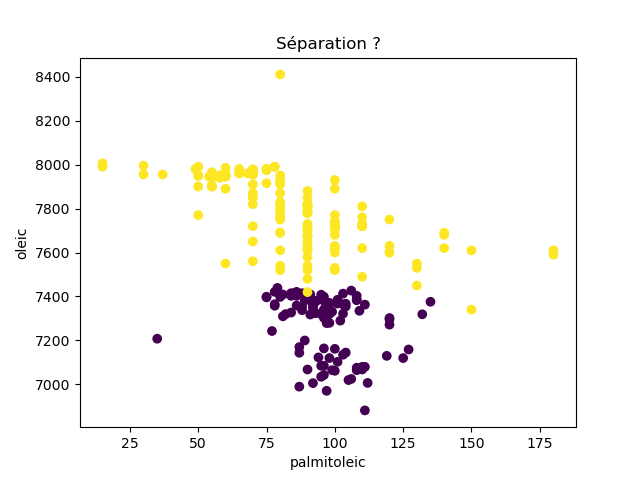
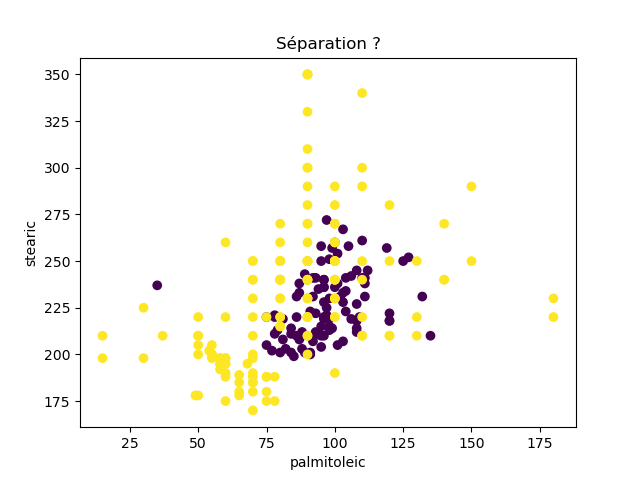
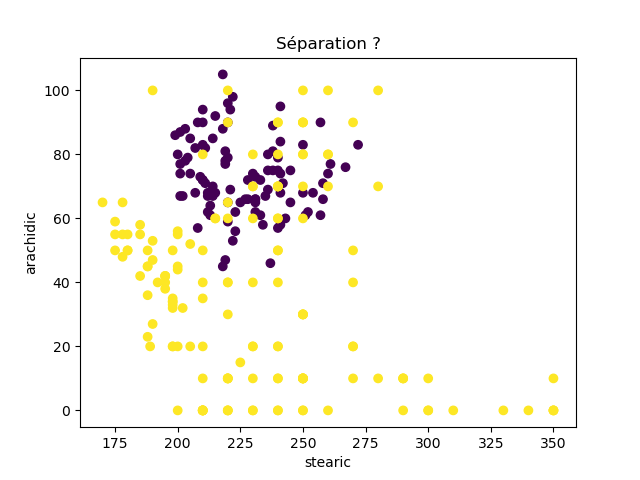
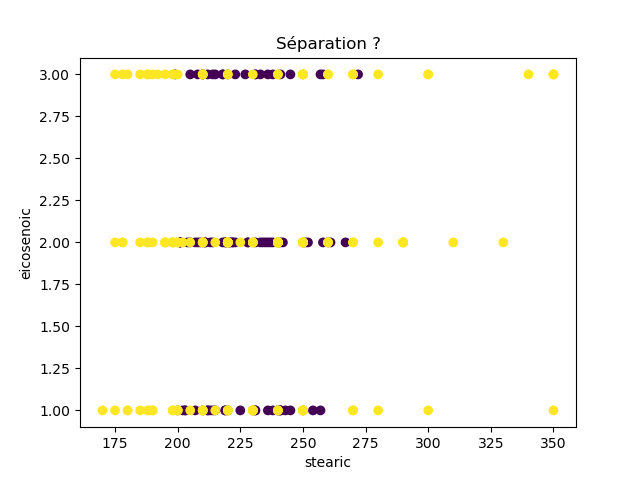
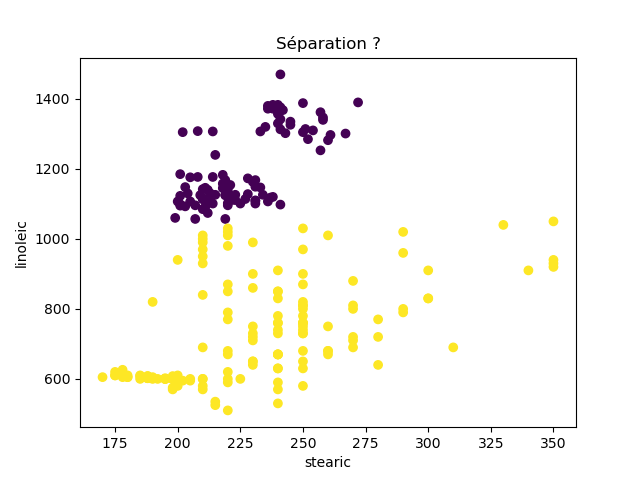
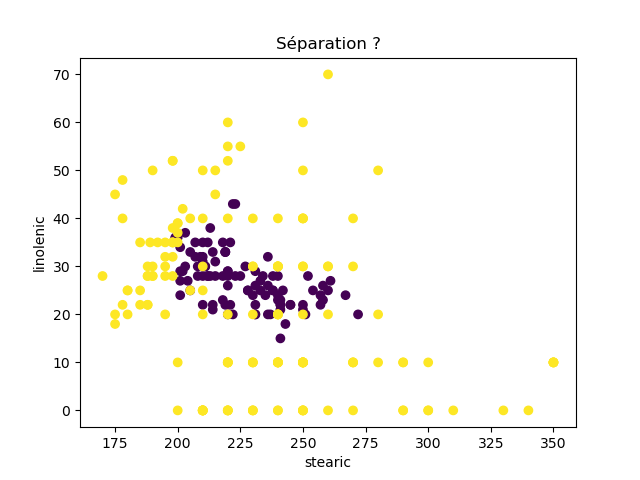
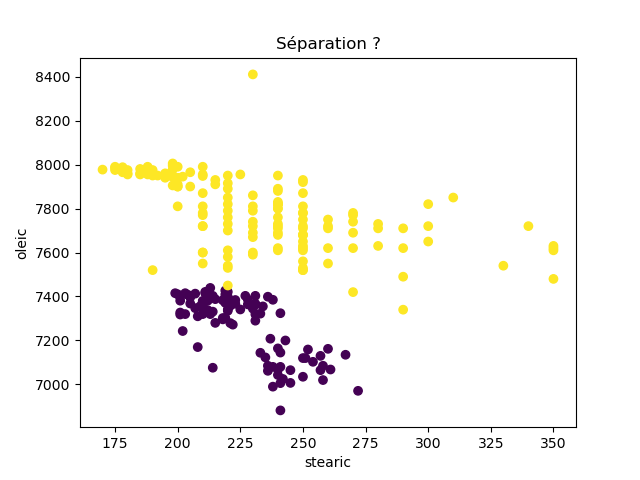
À faire : reproduisez ces 28 graphiques.

Il faut donc trouver un graphique où les points jaunes et les points violets peuvent être séparés par une droite quelconque. La figure ci-dessous illustre l'idée : les données des deux classes sont illustrées par les tâches colorées et on voit que l'on peut séparer les jaunes des bleus par une droite. N'étant ni horizontale ni verticale, cette droite ne peut pas être trouvée par l'algorithme de scikit-learn qui construit des arbres de décision. Par contre, cette droite nous saute aux yeux, ce qui montre encore une fois que l'être humain est bien supérieur à toutes les machines, même celles dont on prétend qu'elles sont intelligentes ;-)
fig
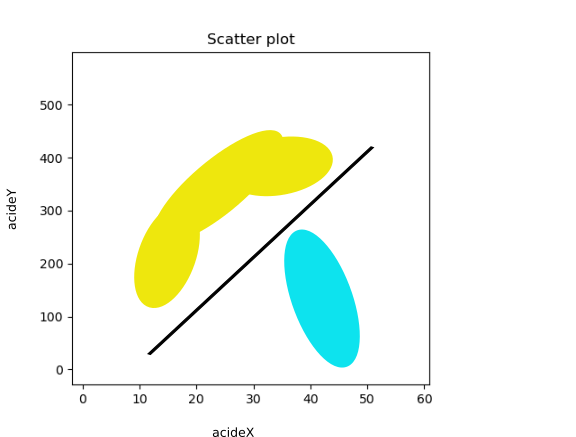
Remarque : toutes ces figures sont symétriques.
Quand on a trouvé une telle paire d'attributs, on détermine l'équation d'une droite qui sépare les deux classes. Comment fait-on ? À l'œil, on détermine deux points par lesquels passent cette droite.
Son équation est de la forme : acideY = a acideX + b, où acideX est l'acide en abscisses, acideY celui en ordonnées, a et b les coefficients de la droite qu'il faut calculer.
Maintenant, on a une règle du genre : si la donnée est en dessous de la droite, alors la classe est bleue, sinon sa classe est jaune. Autrement dit, le signe de acideY - a acideX - b indique la classe.
Dès lors, il suffit d'ajouter un nouvel attribut au jeu de données qui a cette valeur (acideY - a acideX - b) et de construire un arbre de décision avec ce jeu de données augmenté. L'algorithme va utiliser cet attribut pour construire un arbre qui ne fait plus d'erreur, ou du moins, en fait moins. J'obtiens :
fig
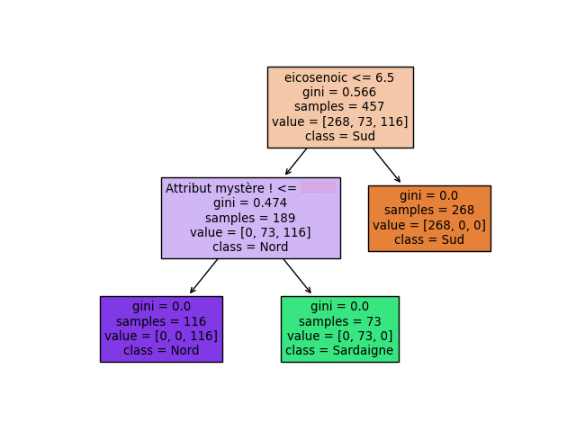
À faire : Faites tout cela et estimez le taux de succès du nouvel arbre de décision.

Plus généralement, notre cerveau est capable de repérer des séparatrices bien plus complexes qu'une simple droite : une courbe parabolique, de degré 3, une courbe en zigzag plus généralement, etc.
En guise d'exercice, supposons qu'il n'y ait pas de paire d'attributs séparant les jaunes des bleus (les olives du Nord de celles de Sardaigne).

À faire :

  1. repérez une paire d'attributs qui semblent séparer les deux classes par une courbe du 2nd degré.
  2. Une courbe du 2nd degré possède 3 coefficients. Cela signifie que nous avons 3 inconnues à déterminer, donc il nous faut 3 points pour les déterminer. À l'œil, déterminez 3 points par lesquels passent cette courbe du 2nd degré.
  3. Poser le problème mathématique à résoudre pour trouver ces 3 inconnues à partir des coordonnées de ces 3 points.
  4. Le résoudre.
  5. En déduire un attribut à ajouter au jeu de données et l'ajouter.
  6. Construire l'arbre de décision avec ce nouveau jeu de données augmenté (n'utilisez pas l'attribut que nous avons précédemment ajouté correspondant à la séparatrice linéaire).
  7. Estimer le taux de succès de ce nouvel arbre de décision.